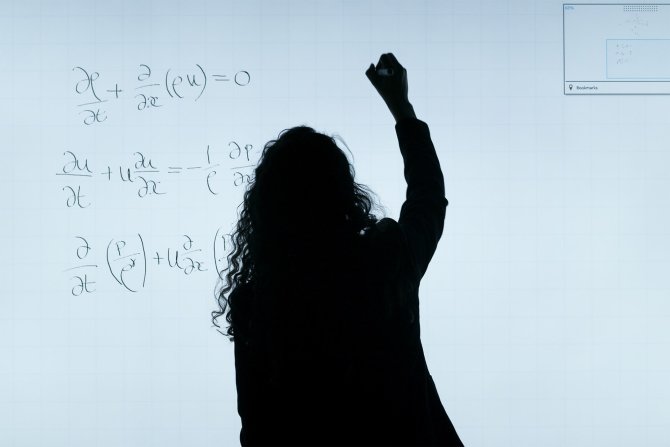Vis dėlto, neseniai už akių užkliuvo laisvai į marškinių kišenę telpanti, bet intriguojanti knyga „Matematika yra mokslo poezija“ (angl. „Mathematics is the poetry of science“), kurioje minėtasis C.Villanis pateikė 10 šių dviejų disciplinų panašumų.
5-iais iš jų dalinamės su 15min skaitytojais. Galbūt beieškant įkvėpimo eilėraščiams, jie padės suprasti poezijos ir matematikos fenomeną?

1. Suvaržymai ir kūrybiškumas
Pasak C.Villanio, matematiką ir poeziją stipriai sieja suvaržymai, kurie yra vieni iš 7 svarbiausių sąlygų kuriant naujas idėjas. Apie pastarąsias mokslininkas kalba savo virtualioje paskaitoje „Pour faire naître une idée“.
Jis sako, kad suvaržymai matematikoje randami beveik visur, mat tai yra taisyklių bei to, ką galima iš jų sukurti, mokslas. Negana to, matematika reikalauja tobulai logiškų sprendimų, kas šiaip jau yra didokas suvaržymas… Taigi turint itin mažą duotųjų (angl. elementary propositions) skaičių, matematikos pagalba galima pateikti didelį kiekį teisingų sprendinių.
Tai C.Villanis susieja su poezijai būdinga prozodija (mokslas apie kirtį), ką galima pavadint vienu žodžiu – eilėdara. Kaip pavyzdį jis pateikia „OuLiPo“ (pranc. „Ouvroir de Littérature Potentielle“) – 1960 metais poeto Raymondo Queneau ir matematiko François Le Lionnais įsteigta rašytojų ir matematikų grupę. Kitaip nei siurrealistai arba dadaistai, pasąmonė arba spontaniškumas „OuLiPo“ nėra įkvėpimo šaltinis. Jie vystė sistemišką ir save varžančią tekstų kūrimo techniką.
Viena žinomiausių – „S + 7 taisyklė“. C.Villanis rašo: jeigu netyčia eilėraštyje randate jums įdomų žodį (gali būti daiktavardis, veiksmažodis ir t.t.), pasižiūrėkite jo reikšmę žodyne. Tada pakeiskite jį į septintąjį po jo einantį žodį ir sukeiskite jį su „išrinktuoju“.
Viena žinomiausių – „S + 7 taisyklė“
Kaip pavyzdį jis pateikia ir prancūzų rašytojo Boriso Viano sukurtus būdus, kuriais siekiama sugretinti nesuderinamus poetinius konceptus. Anot C.Villanio, B.Viano sukurtas skaitinis Dievo skaičiavimas (angl. „numerical calculation of God“) yra beprotiška idėja.
2. Įkvėpimas
Tuo, kad matematiniai konceptai įkvepia poetus ir menininkus, C.Villanis yra užtikrintas, tačiau apie atvirkštinį variantą jis nėra girdėjęs.
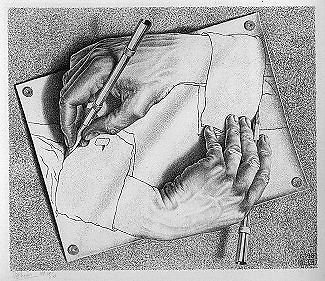
Čia jis pasakoja apie olandų grafikos dizainerį Mauritsą Cornelį Escherį, kurio darbuose atspindimos ir analizuojamos matematinės idėjos. Viena jų, rekursija, perteikiama garsiame jo darbe ir vaizduojam, kaip viena kitą piešiančios rankos. Kita – neeuklidinė geometrija, įkvėpusi jį sukurti besipinančių grindinio akmenų motyvą. Minimas ir reliatyvumas, kuriame tarsi sapne vienas abstraktus konceptas lydi kitą.
C.Villanis pabrėžia, jog M.C.Escheris nesistengia populiarinti matematikos, tai individualūs darbai, kurių įkvėpimu tapo mokslinės idėjos.
3. Ryšių paieškos
Kaip itin poetišką dalyką matematikoje, nepaisant darbo vienumoje ar matematinių taisyklių taikymo literatūroje, C.Villanis išskiria ryšių paieškas.
„Matematikoje [žmogus] amžinai ieško ryšių, analogijų ir palyginimų. Tai yra klasikinis poezijos veikimo būdas“, – rašo jis.
Mokslininko teigimu, sąsajos atlieka svarbų vaidmenį „didingoje matematikos istorijoje“: „Carlas Friedrichas Gaussas, Bernhardas Riemannas, Gregas Lawleris <…> tėra kelios žymios figūros, atradusios sąsajų, apie kurių egzistavimą niekas neturėjo nė minties.“
Jis taip pat teigia, kad Centrinė ribinė teorema (angl. „Central limit theorem“) yra stulbinantis matematinis, o gal net visų mokslų atradimas. Šios teoremos kreivės taip pat vartojamos sintetinant politinę nuomonę, matuojant vandens svyravimus, stebint žmogaus ūgio pokyčius ir t.t.
Abstrakti idėja bando perteikti fizinio pasaulio formų įvairovę.
„Kitaip tariant, abstrakti idėja bando perteikti fizinio pasaulio formų įvairovę“, – teigia C.Villanis, susiedamas šį aspektą su poezija. Jo žodžiais, būtent tai ir glūdi „pačioje poezijos širdyje“.
4. Žodžių forma
Savaime aišku, kad svarbiausia poezijos kūrybinė materija yra žodžiai ir jų forma.
Anot C.Villanio, matematika ir yra kalba, o vėliau priduria, kad tai išskirtinai tiksliųjų mokslų kalba. Ilgainiui ši kalba tapo universalia -vartojama visame pasaulyje.
Tai išskirtinai tiksliųjų mokslų kalba.
5. Kilnojamas pasaulis (angl. A Portable Universe)
Pasaulį, kurį nešiojamės savo galvose, taip pat galime laikyti poezijos ir matematikos panašumu. C.Villanis pasakoja, kad matematikas jį užfiksuoja formulėse, o poetas – posmuose.
Kai kurie realybės aspektai tokie neprieinami, jog gali būti palaikyti pasakomis arba abstrakcijomis.
Mokslininko teigimu, kai kurie realybės aspektai tokie neprieinami, jog gali būti palaikyti pasakomis arba abstrakcijomis. Būtent sutraukdami jas į formules matematikai suteikia galimybę jas apmąstyti. Pavyzdžiui, C.Villanis siūlo pagalvoti apie Jupiterį ir per milijonus šviesmečių atitolusias žvaigždes, kurių niekada nepamtysime, tačiau galime suprasti judėjimą tarp jų. Tai padaryti padeda Isaaco Newtono gravitacijos dėsnis, kuris taip pat leidžia nuspėti tam tikrus dalykus, įvyksiančius ateityje.
Čia C.Villanis analizuoja britų poeto Alfredo Tennysono eilėraštį „The Lady of Shallot“. Knygoje teigiama, jog poetas perpasakoja Artūro laikų legendą apie nelaimingą ir kilmingą jauną moterį. Būdama neteisingai prakeikta, pasaulį jį gali stebėti tik pro veidrodžio refleksiją ir vieną dieną ji pastebi neįtikėtai žavų kunigaikštį serą Lanselotą. Negalėdama susilaikyti nuo tiesioginio žiūrėjimo, ji pasmerkiama mirti.
Pats C.Villanis jauną moterį regi kaip matematikos personifikaciją. Nes matematikai, kitaip nei fizikai, pasaulio negali stebėti tiesiogiai. Jiems reikalinga refleksija arba lygybės.
C.Villanis jauną moterį regi kaip matematikos personifikaciją.
Matematiniai ženklai ne ką mažiau nei poetiniai perteikia reikšmes. Poetai gali jais manipuliuoti, perteikti įspūdžius ir kurti tam tikrus lūkesčius.